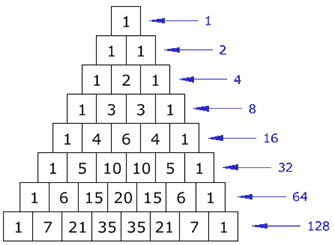
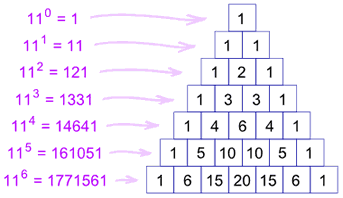
There are many patterns hidden within this triangle. For instance, if you write out the sums of the numbers in each row, you find the numbers double, starting with one, then two, then four, then eight, and so on. Also, if you look at the numbers formed by each row, you find that besides the top each are a multiple of eleven, This starts with 11(11 * 1), then 121(11*11), then 1331(11*121). This works all the way down the triangle, even with a row like 1, 5, 10, 10, 5, 1. Here, you carry over, resulting in the number 161,051(11 * 14641). This pattern is best seen with powers of 11, starting with 110
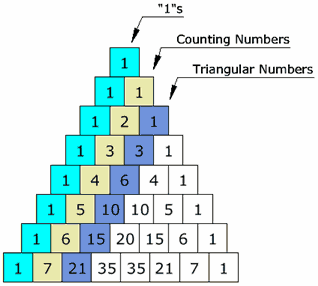
Another interesting thing is if you loom at the diagonals of this triangle. the sums of the numbers in the diagonals will give you the Fibonacci sequence. The diagonals in sequence also have things of interest, the first being ones, the second being counting numbers, the third being triangular numbers, and the fourth being square numbers.

Another strange and interesting thing one can see in this triangle are the Catalan Numbers. The Catalan Numbers are taking shapes and finding out how many triangles it can be divided into by connecting vertices. In Pascal's triangle these numbers are found by taking the even numbers in the center of almost every other row and subtracting the number adjacent to it.
Finally (but not really) If you highlight every even number in Pascal's Triangle, you get a fractal that is essentially Sierpinski's Triangle.

Sources: